¿Qué alternativa estás buscando?
Introduce el término a buscar aquí
Todo tiene una referencia similar con prestaciones similares. Desde los últimos auriculares de apple hasta la aplicación informática que usas cada día.
Informática
Selección de software variado de almacenamiento, limpieza de pc, juegos y mucho más. En ocasiones queremos adquirir el mejor producto pero la barrera suele ser el precio, existen cientos de programas parecidos no tan famosos pero igualmente funcionales.
P2P
Si te gusta disfrutar del cine gratis online seguro que has notado la reciente caída de plataformas que contenían miles de películas y series.
No te preocupes, nuevos portales streaming abren sus puertas al público online. Revisa cada alternativa de los grandes sites de descarga.
Sociedad
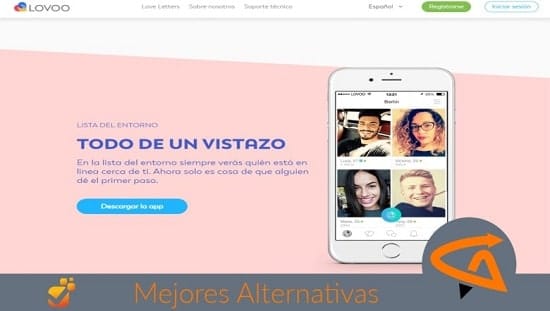
Tenemos cientos de aplicaciones y programas para mejorar la comunicación y acción entre las personas. Sin embargo, casi todos los usuarios escogen las mismas.
Descubre nuevas herramientas muy válidas para comprar online, divertirte, ligar, obtener conocimiento y más.
Edición
Herramientas para editar vídeos, textos, audios y cualquier archivo que exista online. Disfruta de extensos directorios de archivos de edición totalmente gratuitos con las opciones similares que te ofrecemos a continuación:
Electrónica
Convivimos con gadgets y artículos electrónicos que hemos adaptado a nuestro sistema de vida. Las grandes marcas promocionan modelos superiores cada año incrementando su precio, pero poco se habla de marcas genéricas menos conocidas pero con prestaciones similares.
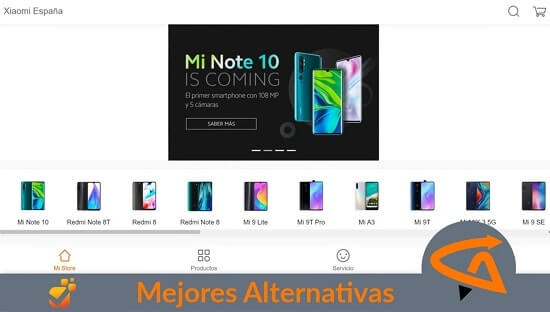
Smartphone
Comparativas de aplicaciones y sistemas operativos para encontrar marcas y modelos de dispositivos móviles no tan conocidos con grandes prestaciones.
La nueva tecnología y conexión de los teléfonos inteligentes están cambiando las comunicaciones, descubre oportunidades gratuitas e incluso mejores que las marcas de renombre.
Streaming
El streaming está de moda, la transferencia de datos es tan alta que cualquier persona con una conexión baja puede disfrutar de casi cualquier película.
Varios
Reviews variadas de los programas más novedosos del mercado